BitMap

相关概念

¶基础类型

在java中：

byte  ->   8 bits  -->  1字节
char  ->   16 bit  -->  2字节
short ->   16 bits -->  2字节
int   ->   32 bits -->  4字节
float ->   32 bits -->  4字节
long  ->   64 bits -->  8字节

¶位运算符

在java中，int数据底层以补码形式存储。int型变量使用32bit存储数据，其中最高位是符号位，0表示正数，1表示负数，可通过Integer.toBinaryString()转换为bit字符串

System.out.println(Integer.toBinaryString(10)); 
System.out.println(Integer.toBinaryString(-10));
// 输出
                            1010
11111111111111111111111111110110

¶左移<<

例如：5 << 2 = 20

将5转为2进制表示形式：   0000 0000 0000 0000 0000 0000 0000 0101  
然后左移2位后，低位补0： 0000 0000 0000 0000 0000 0000 0001 0100  
换算成10进制为20

¶右移>>

例如： 5 >> 2 = 1

将5转为2进制表示形式： 0000 0000 0000 0000 0000 0000 0000 0101 
然后右移2位，高位补0： 0000 0000 0000 0000 0000 0000 0000 0001
换算成十进制后是1

¶无符号右移>>>

例如：5 >>> 3　　　　
在Java中int类型占32位，可以表示一个正数，也可以表示一个负数。正数换算成二进制后的最高位为0，负数的二进制最高为为1。对于2进制补码的加法运算，和平常的计算一样，而且符号位也参与运算，不过最后只保留32位

-5换算成二进制：     1111 1111 1111 1111 1111 1111 1111 1011
-5右移3位：         1111 1111 1111 1111 1111 1111 1111 1111   // (用1进行补位，结果为-1)
-5无符号右移3位：   0001 1111 1111 1111 1111 1111 1111 1111   // (用0进行补位,结果536870911 )

¶位与&

第一个操作数的的第n位于第二个操作数的第n位如果都是1，那么结果的第n为也为1，否则为0

5转换为二进制：0000 0000 0000 0000 0000 0000 0000 0101
3转换为二进制：0000 0000 0000 0000 0000 0000 0000 0011
------------------------------------------------------------
1转换为二进制：0000 0000 0000 0000 0000 0000 0000 0001

¶位或|

第一个操作数的的第n位于第二个操作数的第n位只要有一个为1则为1，否则为0

5转换为二进制：0000 0000 0000 0000 0000 0000 0000 0101
3转换为二进制：0000 0000 0000 0000 0000 0000 0000 0011
-------------------------------------------------------------------------------------
6转换为二进制：0000 0000 0000 0000 0000 0000 0000 0111

对于移位运算，例如将x左移/右移n位，如果x是byte、short、char、int，n会先模32（即n=n%32），然后再进行移位操作。可以这样解释：int类型为32位,移动32位（或以上）没有意义。
同理若x是long，n=n%64。

¶左移和右移代替乘除

a=a*4;
b=b/4;

可以改为

a=a<<2;
b=b>>2;

说明： 　　除2 = 右移1位 乘2 = 左移1位 　　除4 = 右移2位 乘4 = 左移2位 　　除8 = 右移3位 乘8 = 左移3位 　　… …
类比十进制中的满十进一，向左移动小数点后，数字就会缩小十倍，在二进制中满二进一，进行右移一次相当于缩小了2两倍，右移两位相当于缩小了4倍，右移三位相当于缩小了8倍。通常如果需要乘以或除以2的n次方，都可以用移位的方法代替。
实际上，只要是乘以或除以一个整数，均可以用移位的方法得到结果如：
a=a9
分析a9可以拆分成a(8+1)即a8+a1, 因此可以改为： a=(a<<3)+a
a=a7
分析a7可以拆分成a(8-1)即a8-a1, 因此可以改为： a=(a<<3)-a
关于除法读者可以类推, 此略。
【注意】由于+/-运算符优先级比移位运算符高，所以在写公式时候一定要记得添加括号，不可以 a = a*12 等价于 a = a<<3 +a <<2; 要写成a = (a<<3)+(a <<2 )。

¶与运算代替取余

31转换为二进制：011111,0,31
32转换为二进制：100010 与31取交集的结果是：10转换为十进制为2
31转换为二进制：100001 与31取交集的结果是：01转换为十进制为1
30转换为二进制：011110 与31取交集的结果是：11110转换为十进制为30
29转换为二进制：011101 与31取交集的结果是：11101转换为十进制为29
33转换为二进制：100001 与31取交集的结果是：1转换为十进制为1

31转换为二进制后，低位值全部为1，高位全为0。所以和其进行与运算，高位和0与，结果是0，相当于将高位全部截取，截取后的结果肯定小于等于31，地位全部为1，与1与值为其本身，所以相当于对数进行了取余操作。

¶进制转换

• 0x开头表示16进制，例如：0x2表示：2，0x2f表示48
• 0开头表示8进制，例如：02表示：2,010表示：8

Integer.toHexString(int i)   // 十进制转成十六进制
Integer.toOctalString(int i) // 十进制转成八进制 
Integer.toBinaryString(int i)// 十进制转成二进制
Integer.valueOf(m,n).toString() // 把n进制的m转换为10进制

BitMap

¶实现原理

在java中，一个int类型占32个字节，我们用一个int数组来表示时未new int[32],总计占用内存3232bit,现假如我们用int字节码的每一位表示一个数字的话，那么32个数字只需要一个int类型所占内存空间大小就够了，这样在大数据量的情况下会节省很多内存。
具体思路：
　　1个int占4字节即48=32位，那么我们只需要申请一个int数组长度为 int tmp[1+N/32]即可存储完这些数据，其中N代表要进行查找的总数，tmp中的每个元素在内存在占32位可以对应表示十进制数0~31,所以可得到BitMap表:
　　　　tmp[0]:可表示0~31
　　　　tmp[1]:可表示32~63
　　　　tmp[2]可表示64~95
　　　　…
　　那么接下来就看看十进制数如何转换为对应的bit位：
　　假设这40亿int数据为：6,3,8,32,36,…，那么具体的BitMap表示为：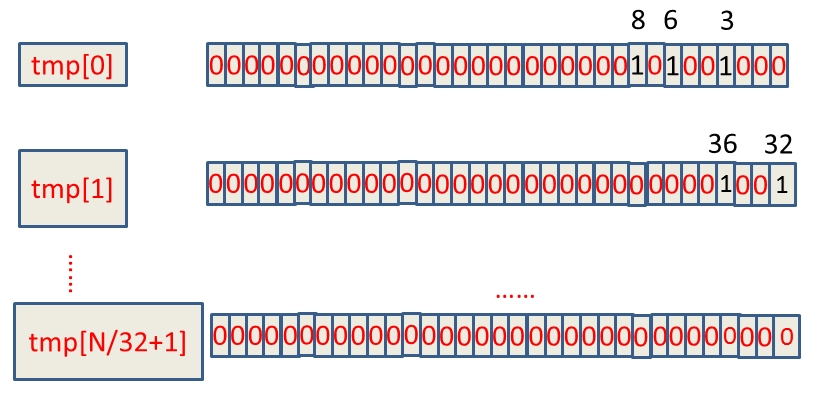

如何判断int数字在tmp数组的哪个下标，这个其实可以通过直接除以32取整数部分，例如：整数8除以32取整等于0，那么8就在tmp[0]上。另外，我们如何知道了8在tmp[0]中的32个位中的哪个位，这种情况直接mod上32就ok，又如整数8，在tmp[0]中的第8 mod上32等于8，那么整数8就在tmp[0]中的第八个bit位（从右边数起）。

¶源码

private long length;
private static int[] bitsMap;
private static final int[] BIT_VALUE = {0x00000001, 0x00000002, 0x00000004, 0x00000008, 0x00000010, 0x00000020,
        0x00000040, 0x00000080, 0x00000100, 0x00000200, 0x00000400, 0x00000800, 0x00001000, 0x00002000, 0x00004000,
        0x00008000, 0x00010000, 0x00020000, 0x00040000, 0x00080000, 0x00100000, 0x00200000, 0x00400000, 0x00800000,
        0x01000000, 0x02000000, 0x04000000, 0x08000000, 0x10000000, 0x20000000, 0x40000000, 0x80000000};

public BitMap2(long length) {
    this.length = length;
    /**
     * 根据长度算出，所需数组大小
     * 当 length%32=0 时大小等于
     * = length/32
     * 当 length%32>0 时大小等于
     * = length/32+l
     */
    bitsMap = new int[(int) (length >> 5) + ((length & 31) > 0 ? 1 : 0)];
}

/**
 * @param n 要被设置的值为n
 */
public void setN(long n) {
    if (n < 0 || n > length) {
        throw new IllegalArgumentException("length value "+n+" is  illegal!");
    }
    // 求出该n所在bitMap的下标,等价于"n/5"
    int index = (int) n>>5;
    // 求出该值的偏移量(求余),等价于"n%31"
    int offset = (int) n & 31;
    /**
     * 等价于
     * int bits = bitsMap[index];
     * bitsMap[index]=bits| BIT_VALUE[offset];
     * 例如,n=3时,设置byte第4个位置为1 （从0开始计数，bitsMap[0]可代表的数为：0~31，从左到右每一个bit位表示一位数）
     * bitsMap[0]=00000000 00000000 00000000 00000000  |  00000000 00000000 00000000 00001000=00000000 00000000 00000000 00000000 00001000
     * 即: bitsMap[0]= 0 | 0x00000008 = 3
     *
     * 例如,n=4时,设置byte第5个位置为1
     * bitsMap[0]=00000000 00000000 00000000 00001000  |  00000000 00000000 00000000 00010000=00000000 00000000 00000000 00000000 00011000
     * 即: bitsMap[0]=3 | 0x00000010 = 12
     */
    bitsMap[index] |= BIT_VALUE[offset];

}
/**
 * 获取值N是否存在
 * @return 1：存在，0：不存在
 */
public int isExist(long n) {
    if (n < 0 || n > length) {
        throw new IllegalArgumentException("length value illegal!");
    }
    int index = (int) n>>5;
    int offset = (int) n & 31;
    int bits = (int) bitsMap[index];
    // System.out.println("n="+n+",index="+index+",offset="+offset+",bits="+Integer.toBinaryString(bitsMap[index]));
    return ((bits & BIT_VALUE[offset])) >>> offset;
}

¶应用

¶看个小场景 > 在3亿个整数中找出不重复的整数，限制内存不足以容纳3亿个整数。

对于这种场景我可以采用2-BitMap来解决，即为每个整数分配2bit，用不同的0、1组合来标识特殊意思，如00表示此整数没有出现过，01表示出现一次，11表示出现过多次，就可以找出重复的整数了，其需要的内存空间是正常BitMap的2倍，为：3亿*2/8/1024/1024=71.5MB。
具体的过程如下：
扫描着3亿个整数，组BitMap，先查看BitMap中的对应位置，如果00则变成01，是01则变成11，是11则保持不变，当将3亿个整数扫描完之后也就是说整个BitMap已经组装完毕。最后查看BitMap将对应位为11的整数输出即可。

¶已知某个文件内包含一些电话号码，每个号码为8位数字，统计不同号码的个数。

8位最多99 999 999，大概需要99m个bit，大概10几m字节的内存即可。 （可以理解为从0-99 999 999的数字，每个数字对应一个Bit位，所以只需要99M个Bit==1.2MBytes，这样，就用了小小的1.2M左右的内存表示了所有的8位数的电话）

¶另一种方式分析BitMap

¶问题引入

bitMap是位图，其实准确的来说，翻译成基于位的映射，举一个例子，有一个无序有界int数组{1,2,5,7},初步估计占用内存44=16字节，这倒是没什么奇怪的，但是假如有10亿个这样的数呢，10亿4字节/(10241024*1024)=3.72G左右（1GB=1024MB 、1MB=1024KB 、1KB=1024B 、1B=8b）。如果这样的一个大的数据做查找和排序，那估计内存也崩溃了，有人说，这些数据可以不用一次性加载，那就是要存盘了，存盘必然消耗IO。我们提倡的是高性能，这个方案直接不考虑。

¶问题分析

如果用BitMap思想来解决的话，就好很多，解决方案如下：
　　一个byte是占8个bit，如果每一个bit的值就是有或者没有，也就是二进制的0或者1，如果用bit的位置代表数组值有还是没有， 那么0代表该数值没有出现过，1代表该数组值出现过。不也能描述数据了吗？具体如下图：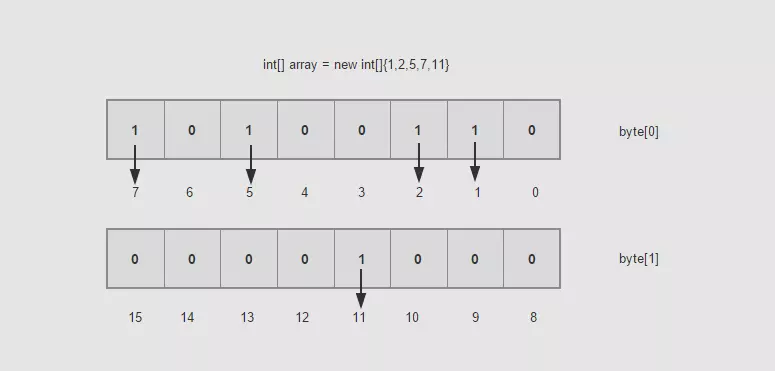

是不是很神奇，那么现在假如10亿的数据所需的空间就是3.72G/32了吧，一个占用32bit的数据现在只占用了1bit，节省了不少的空间，排序就更不用说了，一切显得那么顺利。这样的数据之间没有关联性，要是读取的，你可以用多线程的方式去读取。时间复杂度方面也是O(Max/n)，其中Max为byte[]数组的大小，n为线程大小。

¶应用与代码

如果BitMap仅仅是这个特点，我觉得还不是它的优雅的地方，接下来继续欣赏它的魅力所在。下面的计算思想其实就是针对bit的逻辑运算得到，类似这种逻辑运算的应用场景可以用于权限计算之中。
是不是很神奇，那么现在假如10亿的数据所需的空间就是3.72G/32了吧，一个占用32bit的数据现在只占用了1bit，节省了不少的空间，排序就更不用说了，一切显得那么顺利。这样的数据之间没有关联性，要是读取的，你可以用多线程的方式去读取。时间复杂度方面也是O(Max/n)，其中Max为byte[]数组的大小，n为线程大小。
再看代码之前，我们先搞清楚一个问题，一个数怎么快速定位它的索引号，也就是说搞清楚byte[index]的index是多少，position是哪一位。举个例子吧，例如add(14)。14已经超出byte[0]的映射范围，在byte[1]范围之类。那么怎么快速定位它的索引呢。如果找到它的索引号，又怎么定位它的位置呢。Index(N)代表N的索引号，Position(N)代表N的所在的位置号。

Index(N) = N/8 = N >> 3;
Position(N) = N%8 = N & 0x07;

¶add(int num)

你要向bitmap里add数据该怎么办呢，不用担心，很简单，也很神奇。
上面已经分析了，add的目的是为了将所在的位置从0变成1.其他位置不变.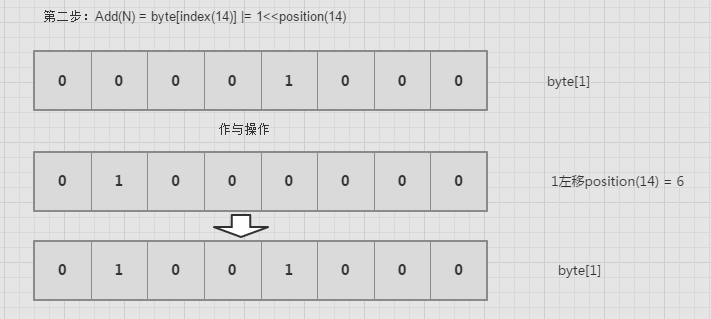

public void add(int num){
    // num/8得到byte[]的index
    int arrayIndex = num >> 3; 
    
    // num%8得到在byte[index]的位置
    int position = num & 0x07; 
    
    //将1左移position后，那个位置自然就是1，然后和以前的数据做|，这样，那个位置就替换成1了。
    bits[arrayIndex] |= 1 << position; 
}

¶clear(int num)

对1进行左移，然后取反，最后与byte[index]作与操作。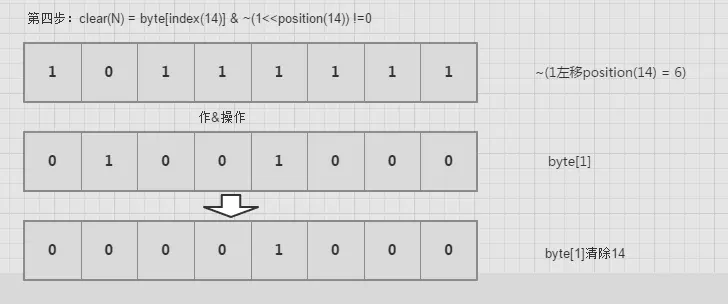

public void clear(int num){
    // num/8得到byte[]的index
    int arrayIndex = num >> 3; 
    
    // num%8得到在byte[index]的位置
    int position = num & 0x07; 
    
    //将1左移position后，那个位置自然就是1，然后对取反，再与当前值做&，即可清除当前的位置了.
    bits[arrayIndex] &= ~(1 << position); 
}

¶contain(int num)

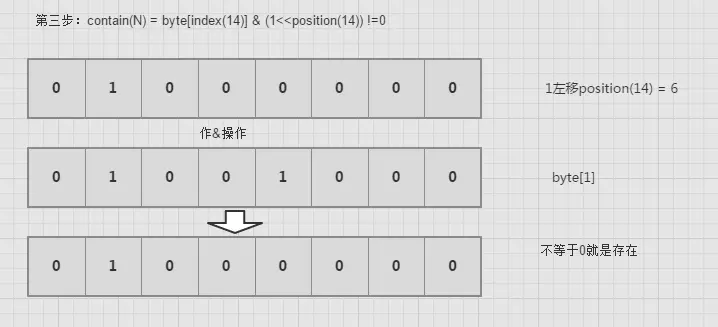
public boolean contain(int num){ // num/8得到byte[]的index
    int arrayIndex = num >> 3; // num%8得到在byte[index]的位置
    int position = num & 0x07; //将1左移position后，那个位置自然就是1，然后和以前的数据做&，判断是否为0即可
    return (bits[arrayIndex] & (1 << position)) !=0; 
}

¶实现

public class BitMap {
    //保存数据的
    private byte[] bits;
    
    //能够存储多少数据
    private int capacity;
    
    
    public BitMap(int capacity){
        this.capacity = capacity;
        
        //1bit能存储8个数据，那么capacity数据需要多少个bit呢，capacity/8+1,右移3位相当于除以8
        bits = new byte[(capacity >>3 )+1];
    }
    
    public void add(int num){
        // num/8得到byte[]的index
        int arrayIndex = num >> 3; 
        
        // num%8得到在byte[index]的位置
        int position = num & 0x07; 
        
        //将1左移position后，那个位置自然就是1，然后和以前的数据做|，这样，那个位置就替换成1了。
        bits[arrayIndex] |= 1 << position; 
    }
    
    public boolean contain(int num){
        // num/8得到byte[]的index
        int arrayIndex = num >> 3; 
        
        // num%8得到在byte[index]的位置
        int position = num & 0x07; 
        
        //将1左移position后，那个位置自然就是1，然后和以前的数据做&，判断是否为0即可
        return (bits[arrayIndex] & (1 << position)) !=0; 
    }
    
    public void clear(int num){
        // num/8得到byte[]的index
        int arrayIndex = num >> 3; 
        
        // num%8得到在byte[index]的位置
        int position = num & 0x07; 
        
        //将1左移position后，那个位置自然就是1，然后对取反，再与当前值做&，即可清除当前的位置了.
        bits[arrayIndex] &= ~(1 << position); 

    }
    
    public static void main(String[] args) {
        BitMap bitmap = new BitMap(100);
        bitmap.add(7);
        System.out.println("插入7成功");
        
        boolean isexsit = bitmap.contain(7);
        System.out.println("7是否存在:"+isexsit);
        
        bitmap.clear(7);
        isexsit = bitmap.contain(7);
        System.out.println("7是否存在:"+isexsit);
    }
}

Roaring Bitmap

¶介绍

对于稀疏的数据，只用bitmap会占用太多内存，比如{1, 2, 3, 200000000}
这样的数据结构会创建200000000 bit来存储，但实际上只有4个数而已，造成大量的内存浪费
为了降低内存的使用，我们经常会使用压缩的位图。
Roaring Bitmaps 是一种压缩的位图，要优于常规的压缩位图，例如 WAH，EWAH 或者 Concise。在某些情况下，可以比它们快几百倍，并且通常提供更好的压缩。

¶主要思想

我们以存放 Integer 值的 Bitmap 来举例，RBM 把一个 32 位的 Integer 划分为高 16 位和低 16 位，通过高 16 位找到该数据存储在哪个桶中（高 16 位可以划分 2^16 个桶），把剩余的低 16 位放入该桶对应的 Container 中。

每个桶都有对应的 Container，不同的 Container 存储方式不同。依据不同的场景，主要有 2 种不同的 Container，分别是 Array Container 和 Bitmap Container。Array Container 存放稀疏的数据，Bitmap Container 存放稠密的数据。若一个 Container 里面的元素数量小于 4096，使用 Array Container 来存储。当 Array Container 超过最大容量 4096 时，会转换为 Bitmap Container。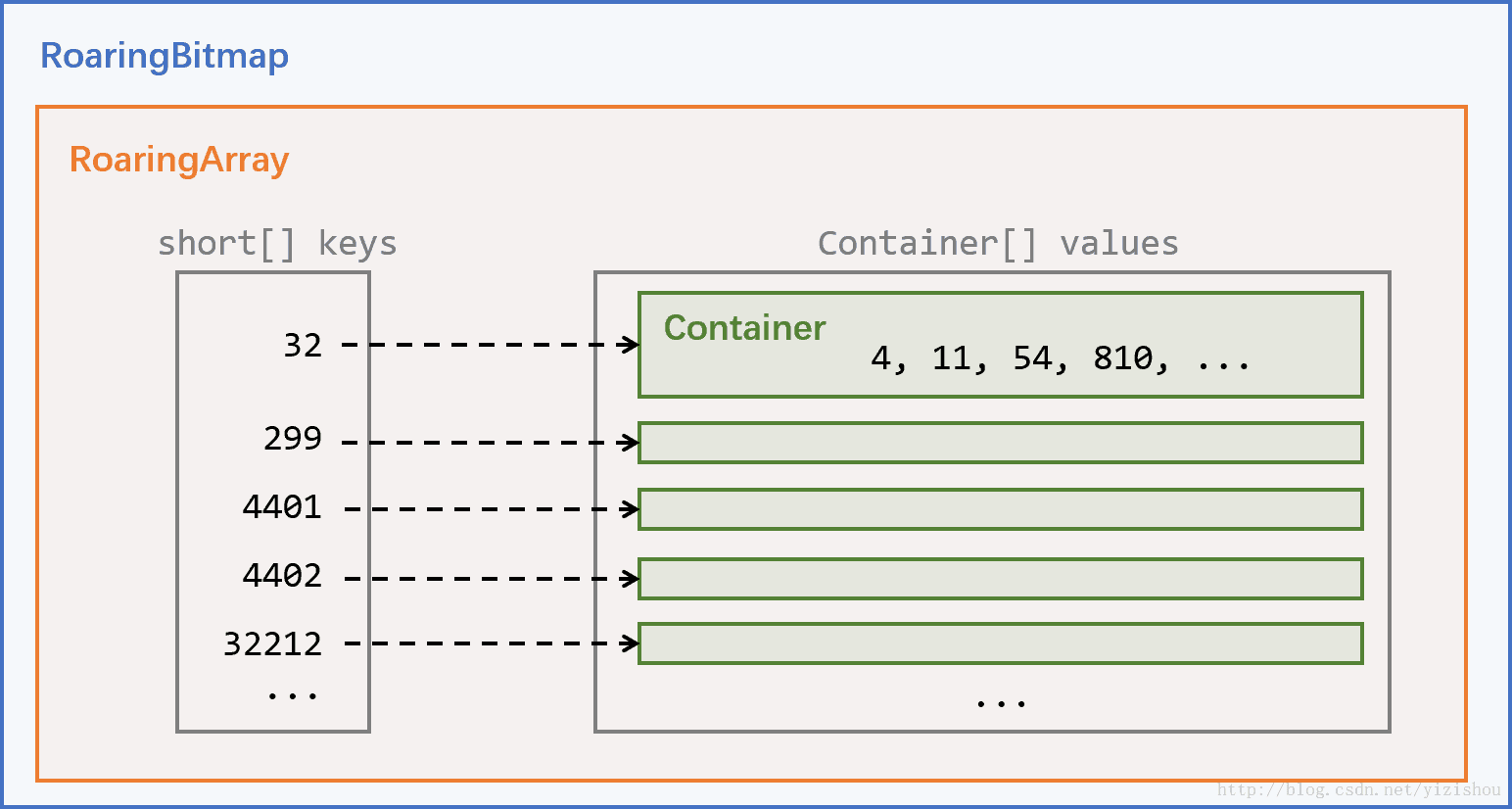

每个RoaringBitmap(GitHub链接)中都包含一个RoaringArray，名字叫highLowContainer。
highLowContainer存储了RoaringBitmap中的全部数据。
RoaringArray highLowContainer;
这个名字意味着，会将32位的整形（int）拆分成高16位和低16位两部分（两个short）来处理。
RoaringArray的数据结构很简单，核心为以下三个成员：

short[] keys;
Container[] values;
int size;

每个32位的整形，高16位会被作为key存储到short[] keys中，低16位则被看做value，存储到Container[] values中的某个Container中。keys和values通过下标一一对应。size则标示了当前包含的key-value pair的数量，即keys和values中有效数据的数量。
keys数组永远保持有序，方便二分查找。

¶Container

RoaringBitmap的核心：三种Container。
通过上面的介绍我们知道，每个32位整形的高16位已经作为key存储在RoaringArray中了，那么Container只需要处理低16位的数据。

¶ArrayContainer

static final int DEFAULT_MAX_SIZE = 4096
short[] content;

结构很简单，只有一个short[] content，将16位value直接存储。
short[] content始终保持有序，方便使用二分查找，且不会存储重复数值。
因为这种Container存储数据没有任何压缩，因此只适合存储少量数据。
ArrayContainer占用的空间大小与存储的数据量为线性关系，每个short为2字节，因此存储了N个数据的ArrayContainer占用空间大致为2N字节。存储一个数据占用2字节，存储4096个数据占用8kb。
根据源码可以看出，常量DEFAULT_MAX_SIZE值为4096，当容量超过这个值的时候会将当前Container替换为BitmapContainer。

¶BitmapContainer

final long[] bitmap;

这种Container使用long[]存储位图数据。我们知道，每个Container处理16位整形的数据，也就是0~65535，因此根据位图的原理，需要65536个比特来存储数据，每个比特位用1来表示有，0来表示无。每个long有64位，因此需要1024个long来提供65536个比特。
因此，每个BitmapContainer在构建时就会初始化长度为1024的long[]。这就意味着，不管一个BitmapContainer中只存储了1个数据还是存储了65536个数据，占用的空间都是同样的8kb。

¶RunContainer

private short[] valueslength;
int nbrruns = 0;

RunContainer中的Run指的是行程长度压缩算法(Run Length Encoding)，对连续数据有比较好的压缩效果。
它的原理是，对于连续出现的数字，只记录初始数字和后续数量。即：

• 对于数列11，它会压缩为11,0；
• 对于数列11,12,13,14,15，它会压缩为11,4；
• 对于数列11,12,13,14,15,21,22，它会压缩为11,4,21,1；
  这种压缩算法的性能和数据的连续性（紧凑性）关系极为密切，对于连续的100个short，它能从200字节压缩为4字节，但对于完全不连续的100个short，编码完之后反而会从200字节变为400字节。
  如果要分析RunContainer的容量，我们可以做下面两种极端的假设：
• 最好情况，即只存在一个数据或只存在一串连续数字，那么只会存储2个short，占用4字节
• 最坏情况，0~65535的范围内填充所有的奇数位（或所有偶数位），需要存储65536个short，128kb

¶Container性能总结

¶读取时间

只有BitmapContainer可根据下标直接寻址，复杂度为O(1)，ArrayContainer和RunContainer都需要二分查找，复杂度O(log n)

¶内存占用

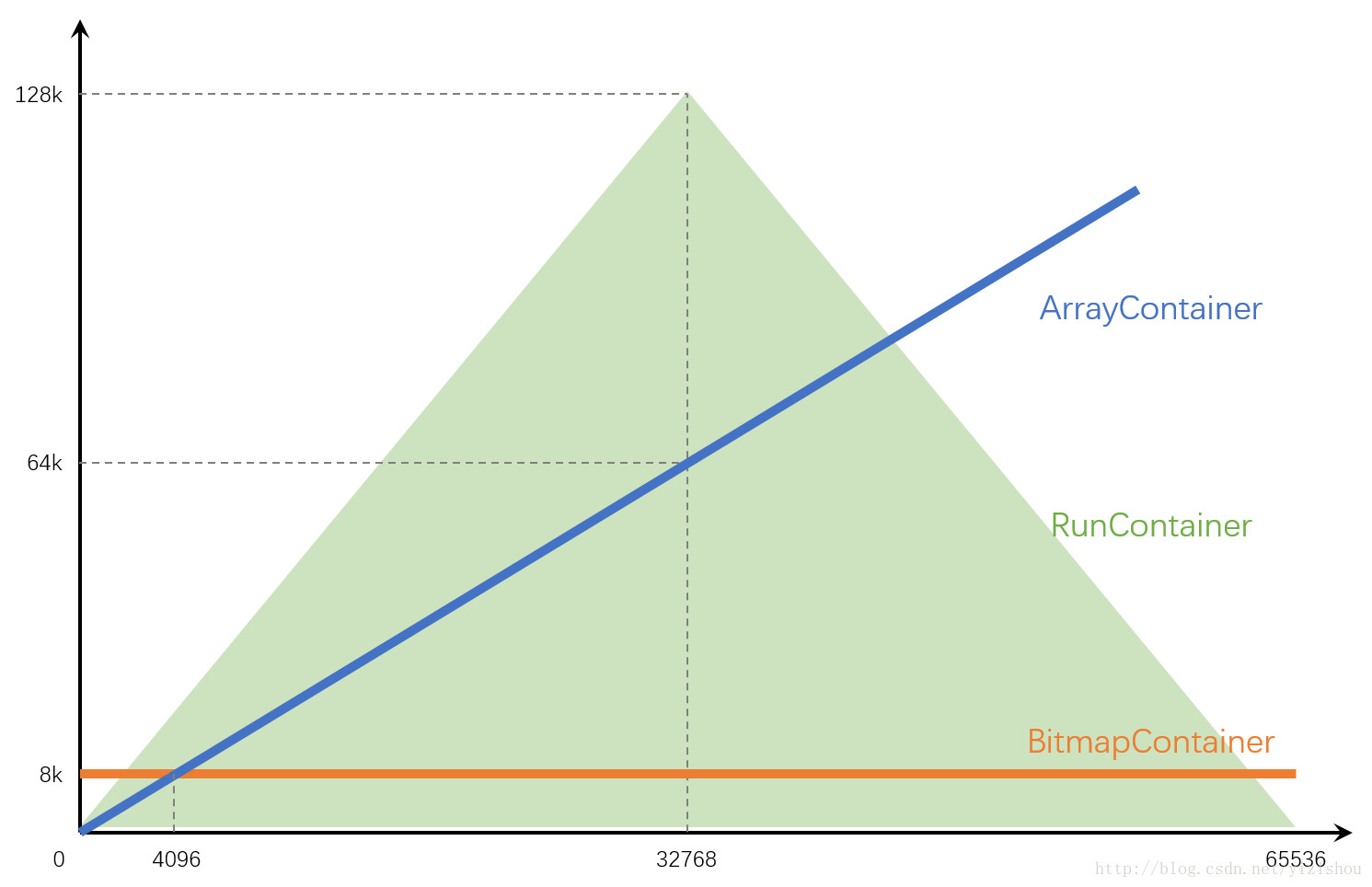
这张图一张图，大致描绘了各Container占用空间随数据量的趋势。
其中

• ArrayContainer一直线性增长，在达到4096后就完全比不上BitmapContainer了
• BitmapContainer是一条横线，始终占用8kb
• RunContainer比较奇葩，因为和数据的连续性关系太大，因此只能画出一个上下限范围。不管数据量多少，下限始终是4字节；上限在最极端的情况下可以达到128kb。

¶RoaringBitmap针对Container的优化策略

创建时：

• 创建包含单个值的Container时，选用ArrayContainer
• 创建包含一串连续值的Container时，比较ArrayContainer和RunContainer，选取空间占用较少的

转换：
针对ArrayContainer：

• 如果插入值后容量超过4096，则自动转换为BitmapContainer。因此正常使用的情况下不会出现容量超过4096的ArrayContainer。
• 调用runOptimize()方法时，会比较和RunContainer的空间占用大小，选择是否转换为RunContainer。

针对BitmapContainer：

• 如果删除某值后容量低至4096，则会自动转换为ArrayContainer。因此正常使用的情况下不会出现容量小于4096的BitmapContainer。
• 调用runOptimize()方法时，会比较和RunContainer的空间占用大小，选择是否转换为RunContainer。

针对RunContainer：

• 只有在调用runOptimize()方法才会发生转换，会分别和ArrayContainer、BitmapContainer比较空间占用大小，然后选择是否转换。